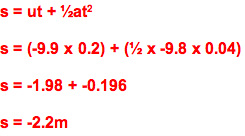SUVAT Equations
You need to learn the equations below
s = displacement (distance with direction - a particle can travel 30m but still have a displacement of 0m if it returns back to its starting position)
u = starting velocity (speed with direction)
v = final velocity (speed with direction - can have minus velocity)
a = acceleration (also has direction - deceleration is acceleration in the opposite direction to the direction of travel)
t = time
In mechanics the signs (+ or -) need to be viewed as direction not as size
Positive direction is generally accepted to be right up the x axis and up the y axis
Negative direction is generally accepted to be left down the x axis and down the y axis
u = starting velocity (speed with direction)
v = final velocity (speed with direction - can have minus velocity)
a = acceleration (also has direction - deceleration is acceleration in the opposite direction to the direction of travel)
t = time
In mechanics the signs (+ or -) need to be viewed as direction not as size
Positive direction is generally accepted to be right up the x axis and up the y axis
Negative direction is generally accepted to be left down the x axis and down the y axis
For example:
Acceleration in Straight Line Kinetics
Unless told otherwise a particle will continue at the same acceleration
If a particle is accelerating in the negative direction but traveling with a positive velocity the particle will decelerate
However once the velocity reaches zero the particle is still accelerating in the negative direction so it will then start traveling in the negative direction
If a particle is accelerating in the negative direction but traveling with a positive velocity the particle will decelerate
However once the velocity reaches zero the particle is still accelerating in the negative direction so it will then start traveling in the negative direction
For particle P from O to T:
s = ?m
u = 8m/s
v = 0m/s
a = -2m/s^2
t = ?s
To find out the maximum displacement (achieved at T when the particle travels no further):
s = ?m
u = 8m/s
v = 0m/s
a = -2m/s^2
t = ?s
To find out the maximum displacement (achieved at T when the particle travels no further):
Because the rate of change in velocity (acceleration) is the same at all times we can assume things are the same on the journey back to O.
From O to T = 16m
From T to O = -16m
This means the displacement of particle P from O back to O is 0m
In this case every point from O to T the particle has two velocities of equal magnitude but opposite direction
What's different is the time.
To work out the time taken to get from O to O use:
s = 0m
u = 8m/s
v = -8m/s
a = -2m/s^2
t = ?s
From O to T = 16m
From T to O = -16m
This means the displacement of particle P from O back to O is 0m
In this case every point from O to T the particle has two velocities of equal magnitude but opposite direction
What's different is the time.
To work out the time taken to get from O to O use:
s = 0m
u = 8m/s
v = -8m/s
a = -2m/s^2
t = ?s
From being told that a particle started at O traveling at 8 m/s decelerating at 2 m/s^2 we have been able to deduce that the:
If given the displacement of A or the time the particle arrives at A we can deduce the velocity at A
- Maximum displacement from O in positive direction is 16m
- The velocity at point O can be 8 m/s and -8 m/s at different times (t = 0 and t = 8)
- The time it takes for particle P to return to O is 8s
If given the displacement of A or the time the particle arrives at A we can deduce the velocity at A
Acceleration and Gravity
Gravity makes an object accelerate as it is a force
Gravity provides a downward acceleration of 9.8 m/s^2
Gravity provides a downward acceleration of 9.8 m/s^2
In the vertical plain works in exactly the same way as in a horizontal line except we don't need to be told as much.
S to T is 5m and S to G takes 0.2s
We need to find out what the starting velocity of P is at S
At first look we've only been told one thing about T. However we know much more:
s = 5m
u = ?m/s
v = 0m/s (because T is the turning point)
a = -9.8m/s^2 (due to gravity)
t = ?s
We need to find out what the starting velocity of P is at S
At first look we've only been told one thing about T. However we know much more:
s = 5m
u = ?m/s
v = 0m/s (because T is the turning point)
a = -9.8m/s^2 (due to gravity)
t = ?s
To find out 'u' use:
To find the height P started off the ground use:
s = ?m
u = -9.9m/s
v = ?m/s
a = -9.8m/s^2
t = 0.2s
s = ?m
u = -9.9m/s
v = ?m/s
a = -9.8m/s^2
t = 0.2s
Use:
This means the particle started 2.2m above G
Two particles
When asked to work out when two particles match each other's displacement, velocity etc. you need to use simultaneous equations.
E.g.
Particle P is traveling at a constant velocity of 5m/s
3 seconds later Particle Q sets off from the same place and accelerates at a constant rate of 3m/s^2
How long after Q starts does Q overtake P?
First right down the information you know that starts from t = 3
P
s = ?
u = 5
v = 5
a = 0
t = ?
Q
s = ?
u = 0
v = ?
a = 3
t = ?
This means you want an equation without v in it
E.g.
Particle P is traveling at a constant velocity of 5m/s
3 seconds later Particle Q sets off from the same place and accelerates at a constant rate of 3m/s^2
How long after Q starts does Q overtake P?
First right down the information you know that starts from t = 3
P
s = ?
u = 5
v = 5
a = 0
t = ?
Q
s = ?
u = 0
v = ?
a = 3
t = ?
This means you want an equation without v in it
Kinetic Graphs
Graphs are a good way of working out questions with two particles. This helps you plot where they meet each other.