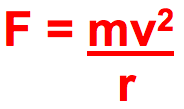Circular Motion

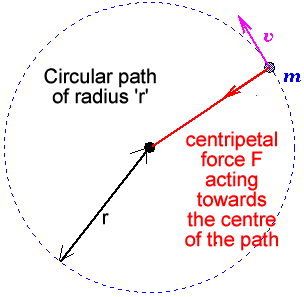
Circular motion is when a force is applied to an object perpendicular to travel creating a circular motion path

In circular motion there is:

• The mass 'm'
• The 'r' the radius (from the centre of circle)
• The centripetal force 'F' pulling the mass towards the centre of the circle, perpendicular to the direction of travel
• The centripetal acceleration 'a' of the mass once the centripetal force is applied i the acceleration towards the centre of the circle
• The instantaneous velocity 'v', which is the speed of the mass once the centripetal force is removed
• The periodic time 'T', the time for one oscillation
  

Working out Instantaneous Speed

The instantaneous speed is the speed (not velocity) of the mass if no centripetal force was applied

Working out Centripetal Acceleration

To understand centripetal acceleration - think about the forces being applied

If an object is traveling in a straight line then there is no force being applied perpendicular to travel.

Once a centripetal force is applied, using F = ma, there must be acceleration

This means the object is in constant acceleration towards the centre of the circle

To work this out the equation below is applied

Working out Centripetal Force

By inserting acceleration into F = ma we get:

Note: Centrifugal force is the opposition force to the centripetal force. It is the inertia of the object

When working out questions for the centripetal force, if the radius is constant then the centrifugal force must equal the centripetal force. 

The centrifugal force of an object is its weight (mg)

Radians

Radians are a measure of an angle

They are more important in A2 and were explained in AS Maths here

Conical Pendulums

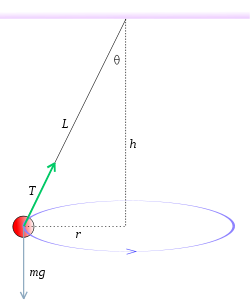
Conical pendulums are masses traveling in circular motion whilst hanging from a point placed vertically above

Only two forces acting on the mass. Weight and tension in the string

The reason the mass travels in a circular shape is because of the tension in the string is applying enough force vertically to equal the weight and create a centripetal force.

This means

Tcosθ = mg (because there is no acceleration vertically)

Tsinθ = centripetal force